概要
一般に、アクティブ・クランプ方式のフォワード・コンバータでは、PMOSを使用してクランプ動作を実現します。そして、この電源トポロジを採用すれば高い効率が得られると認識されています。実際、同方式のフォワード・コンバータでは、インダクタンスに蓄積したエネルギーをグリッドにフィードバックすることができます。そのため、コンバータ全体としての効率を高められます。また、効率を更に向上させるために、2次側の回路としてMOSFETを利用した自己整流回路が用いられるケースがあります。本稿では、この2次側の整流回路を設計する際に直面する課題について解説します。特に、デューティ・サイクルの最適化によってどのような効果が得られるのかを明らかにします。なお、アクティブ・クランプ方式のフォワード・コンバータには多様な電源技術が適用されます。本稿で説明する技術はその一例です。
はじめに
アクティブ・クランプ方式のフォワード・コンバータ(以下、ACFC)では、デューティ・サイクルが出力電圧と効率に関する重要なパラメータになります。一般に、フォワード・コンバータのデューティ・サイクルは最大50%に制限されます。ただ、ACFCでは、50%以上のデューティ・サイクルを利用することができます。
ACFCと最大デューティ・サイクルの関係について記された文献は数多く公開されています。それに対し、最小デューティ・サイクルを用いる設計について解説した文献はあまり存在しません。そこで本稿では、最小デューティ・サイクルが設計に与える影響について解説することにします。その解説に向けて、本稿では絶縁型ACFCの例を取り上げます。その絶縁型ACFCを使用すれば、24VACまたは48VDCの入力電圧を基に、60VDC/1.5Aの出力を生成できます。絶縁機能を備えていることから、産業分野のアプリケーションに適したものだと言えます。このACFCは、そのトポロジによって最大91%のピーク効率を達成します。表1に、このACFCの設計仕様を示しました。
| パラメータ | 記号 | 最小 | 最大 |
| 入力電圧 | VINDC | 27.8 VDC (≈ 24 × 85% × √2-1) | 60 VDC |
| VINAC | 20.4 VAC (≈ 24 × 85%) | 41.8 VAC | |
| スイッチング周波数 | 350 kHz | ||
| ピーク周波数 | η | Higher than 88% | |
| デューティ・サイクル | D | 0.22 | 0.46 |
| 出力電圧 | VOUT | 14.85 | 15.15 |
| 出力電圧リップル | ΔVOUT | 300 mV | |
| 出力電流 | IOUT | 0 A | 1.5 A |
| 出力電力 | POUT | 22.5 W | |
アナログ・デバイセズの「MAX17598」は、アクティブ・クランプ電流モードに対応するPWM(Pulse Width Modulation)コントローラです。この製品は、絶縁型のフォワード・コンバータをベースとする電源の設計に必要なすべての制御回路を備えています。本稿では、その電源の2次側で使用する自己整流回路について解説します。具体的には、その回路を設計する際に考慮すべき事柄を明らかにします。その上で、設計後の回路の評価結果を示します。
2次側の自己整流回路を設計する際に考慮すべき事柄
ACFCに自己整流回路を適用すれば、より高い効率が得られます。図1に、MOSFETを使用した一般的な自己整流回路の例を示しました。ダイオードを用いる従来の整流回路と比べると、MOSFETを使用した回路では、より低いオン抵抗を活かすことができます。特に、電圧が低く出力電流が多い場合にはより高い効率が得られます。


但し、この回路は出力電圧がMOSFETを駆動するゲート電圧に近いかそれを超える場合にはうまく機能しません。この問題を回避するために、MOSFETのゲートを駆動する電圧を生成するために追加の回路を使用するケースがあります。図2に示したのがその回路の例です。この回路のG1とG2は、トランスの補助巻線に接続します。
ゲート1は、図1のトランジスタN2のゲートにリンクされます。一方、ゲート2はトランジスタN1のゲートにリンクされます。ゲート1とゲート2は、スイッチング・サイクルに同期して動作します。ゲート1の出力がハイの場合、ゲート2はローを出力します。ゲート1の出力がローの場合、ゲート2はハイを出力します。図3に、ACFCをベースとする電源回路全体を示しました。本稿の後半では、この回路の評価結果などを示すことにします。
この回路では、出力がMOSFETを駆動可能なVGSの範囲内にあることを保証しなければなりません。以下の式は、ゲートを駆動する電圧と巻数比の関係を表しています。
ここで、KGATEはトランスの変圧比です。NGはトランスの巻線の巻数であり、NPはトランスの1次巻線の巻数を表します。VGATE_MAXは、MOSFETのゲートを駆動する電圧の最大値です。VDC_MAXは、DC入力電圧の最大値です。
1次ループのメインのスイッチがオンのとき、トランスに印加されるのは正の電圧VDCです。このとき、ゲート1の出力はハイ、ゲート2の出力はグラウンドのレベルになります。ゲート1の出力は、巻数比とDC入力電圧に依存します(以下参照)。
メインのMOSFETがオフのとき、クランプ回路はドレイン電圧をVCLAMPに制限します。VCLAMPはVDCより高いため、ゲート1の出力はグラウンドのレベル、ゲート2はハイになります。
クランプ電圧は次式によって求められます。
ゲート2の電圧は、巻数比ならびにVCLAMPとVDCINPUTの電位差に依存します(以下参照)。
デューティ・サイクルは入力電圧に応じて変化します。そのため、ゲートを駆動する電圧が、VINの範囲全体にわたって確実にMOSFETを駆動できるようにすることが重要です。最大のDC入力電圧と最小のオン・レートが与えられたとき、ゲートを駆動する電圧は最小値に達します。
図3の設計において、ゲート2の最小電圧は以下のようにして求められます。ご覧のように、DC入力電圧が最大値に達したとき、ゲート2の電圧はわずか4.23Vです。
この電圧がVGSの閾値より低い場合、2次側の整流回路のMOSFETは適切に動作しません。そのため、入力電圧が最大値に近い場合、電源回路は負荷がなければ起動しないという問題が生じます。図3の回路では、VGSの閾値電圧は3Vで、VGATE2の計算値より低くなっています。
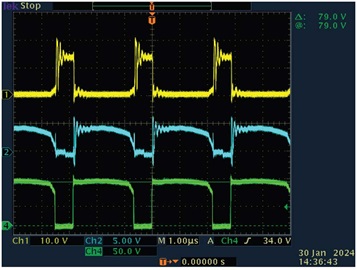
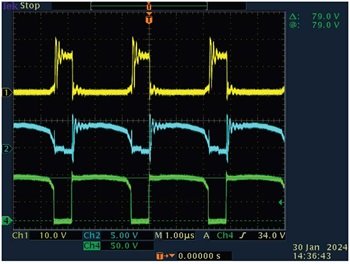
図4に、図3の回路の信号波形を示しました。図中のCh1は、ゲート1の電圧を表しています。同Ch2に表示されているのはゲート2の電圧です。同Ch4は、1次側のNMOSのソース‐ドレイン電圧を表しています。
図3の回路の性能
ゲートを駆動する回路に関する計算が正しいことを確認するために、図3の回路の性能を評価しました。図5は、負荷電流が0A、0.5A、1A、1.5Aの場合の入力電圧と出力電圧をプロットしたものです。
図6は、出力電流が異なる場合に出力電圧のレベルがどのように変化するのかを表しています。各プロットは、異なる入力電圧に対応しています。
図7は、入力電圧と負荷を変化させた場合のピーク効率をプロットしたものです。出力が1.5A、入力が36Vの場合に、ピーク効率は91%に達します。
図8のボード線図は、ループ応答を表しています。図3の回路は、VDCINPUTが36V、IOUTPUTが1.5Aという条件でピーク効率を達成します。
図8は、この動作条件におけるループの安定性を表しています。.
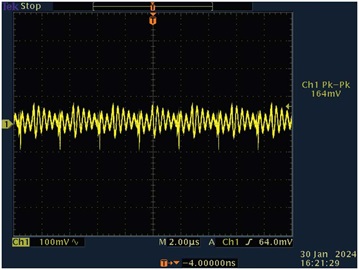
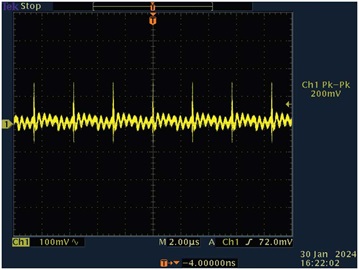
図9と図10は、出力のピークtoピーク電圧を表したものです。図9は無負荷の場合、図10は全負荷の場合の結果です。
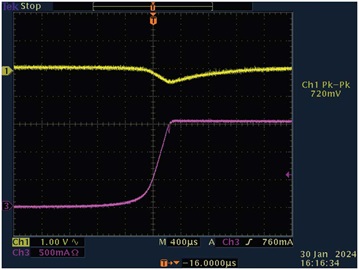
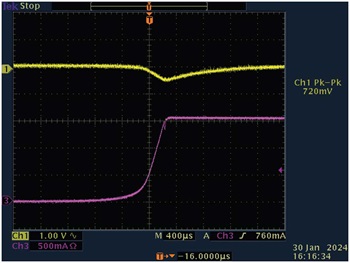
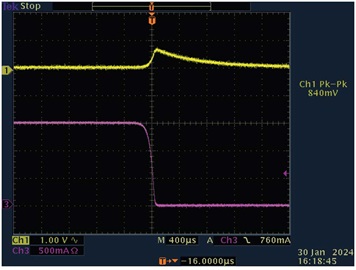
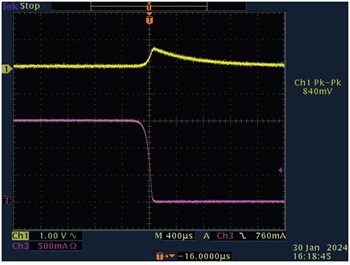
図11と図12は、負荷過渡応答を表しています。図11は、無負荷から全負荷まで変化させた場合の結果です。一方の図12は、全負荷から無負荷に変化させた場合の結果です。図中のCh1は出力電圧(ACカップリング)、同Ch2は出力負荷電流を表しています。
まとめ
本稿では、ACFCについて詳しく検討しました。それにより、性能と効率に関する重要な洞察が得られました。本稿で重点を置いたのは、2次側の整流回路の設計とデューティ・サイクルの影響についてです。その結果、補助用のゲート駆動回路を追加する必要がある場合の最小デューティ・サイクルが明らかになりました。
ACFCは、エネルギーを再利用できるという固有の特徴を備えています。そのため、効率の高い電源システムが必要な場合の有力な選択肢になり得ます。本稿で説明したとおり、デューティ・サイクルに最適な範囲があることは明らかです。MOSFETを使用した整流回路においては、デューティ・サイクルの最大値と最小値の両方が重要な意味を持ちます。
本稿で示した検討結果をACFCの設計や実装に反映させれば、設計段階における問題を回避することが可能になります。
参考資料
1 「Designing Active-Clamp Forward Converters Using Peak-Current-Mode Controllers(ピーク電流モードのコントローラを使用し、アクティブ・クランプ方式のフォワード・コンバータを設計する)」Analog Devices、2014年8月