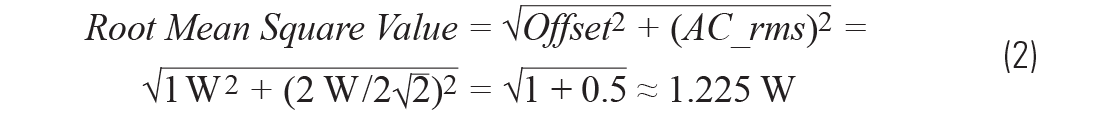質問:
信号やシステム、デバイスに関連してAC電力を扱うケースがあります。その場合、電力の値は2乗平均平方根(RMS:Root Mean Square)を使用して表記するべきなのですか?

回答:
RMS電力をどのように定義するかによります。
AC電力波形のRMS値を計算するのは、好ましいとは言えません。その値は物理的な意味を持たないからです。
平均電力を計算する場合には、電圧と電流のRMS値を使用するとよいでしょう。その結果には意味があるからです。
説明
1Ωの抵抗の両端に、1Vrmsで正弦波形の電圧を印加すると、どれだけの電力が消費されるでしょうか。その答えは以下のとおりです。

これは十分に理解されている問題であり1、議論の余地はありません。
ここで、上記の値とRMS電力の計算値を比較してみましょう。
図1に示したのは、1Vrmsの正弦波のグラフです。ピークtoピークの電圧は1Vrms×2√2 = 2.828Vであり、値の範囲は1.414V~-1.414Vです2。

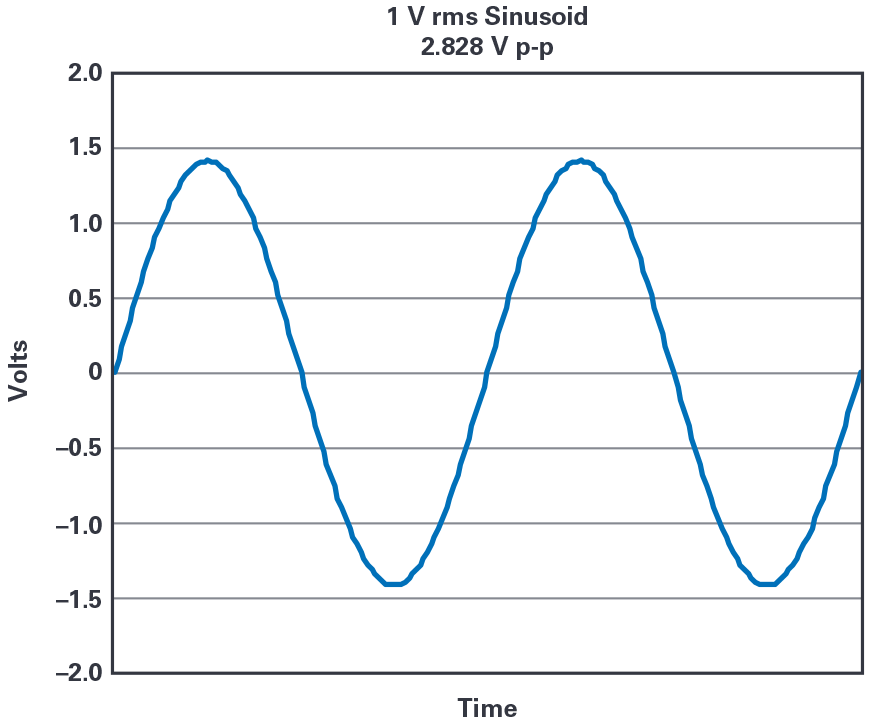
図2に示したのは、この1Vrmsの正弦波を1Ωの抵抗の両端に印加した場合の消費電力(P = V2/R)です。このグラフからは、以下のようなことがわかります。

- 瞬時電力の曲線のオフセットは 1W で、範囲は 0W ~ 2W です。
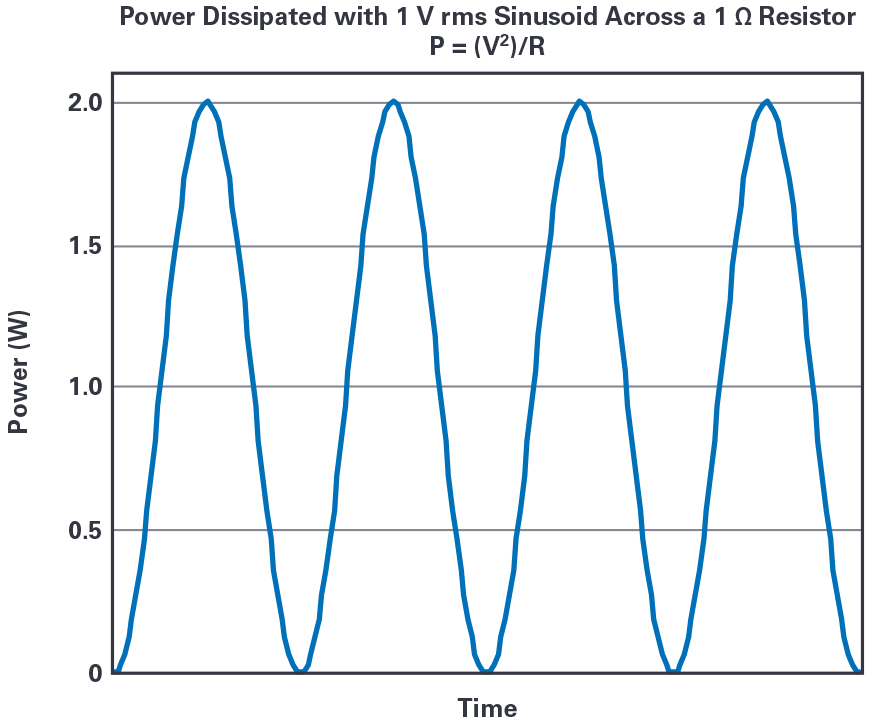
- この電力波形の RMS 値は 1.225W です。
- この電力波形の平均値は 1W です。このことは、グラフを見れば明らかです。1V の上側と下側で波形が対称形を成しているからです。波形のデータポイントを基に平均値を計算しても、同じ結果が得られます。
- 平均電力の値は、RMS 電圧を用いて計算した電力の値と一致します。
1Vrmsの正弦波を1Ωの抵抗の両端に印加した場合の消費電力は1Wです。1.225Wではありません。つまり、平均電力の値は正しく、物理的な意味があるのは平均電力だということです。(ここで定義するところの)RMS電力の計算は、演習として行っているというだけで、明確に有用な意味(明確な物理的/電気的意義)はありません。
1Armsの正弦波形の電流を1Ωの抵抗に流した場合、同じ解析を行うとどうなるでしょうか。その答えは自明であり、同じ結果が得られます。
一般に、ICの電源にはDC電圧が使用されます。そのため、ICの消費電力について検討する際、RMS電力を導入する必要はありません。電源がDC電圧である場合、平均値とRMS値は同じ値になります。本稿で定義するところのRMS電力ではなく、平均電力を使用することが重要になるのは、電圧と電流が時間の経過に伴い変化する場合です。ノイズ、RF信号、発振器などがこれに該当します。
RMS電圧やRMS電流を使用して平均電力を計算してください。そうすれば、意味のある電力値が得られます。
1 抵抗の両端に印加した電圧と消費電力の基本的な関係は、オームの法則(V = IR)、電圧の基本的な定義([エネルギー]÷[単位電荷])、電流の基本的な定義([単位電荷]÷[時間])から簡単に導くことができます。[電圧]×[電流] = [エネルギー]÷[時間] = [電力]です。
2 正弦波のピークtoピーク振幅は、RMS値に2√2を乗じた値になります。正弦波形の電圧の場合、Vp-p = Vrms×2√2です。ここで、Vp-pはピークtoピーク電圧、VrmsはRMS電圧です。これはよく知られている関係であり、数え切れないほど多くの教科書に記載されています。en.wikipedia.org/wiki/Root_mean_squareにも同様の記載があります。
3 これは、一定のDCオフセット値と、それとは別のACのRMS値を基にRMS値を計算するというものです。Keysight Technologiesのアプリケーション・ノート「Make Better ACR MS Measurements with Your Digital Multimeter(デジタルマルチメータを使用してより良いAC実効値測定を行うためのヒント」に記載されています。
4 教科書に載っている標準的な定義が、より詳しい公式の1つの例になります(以下参照)。