概要
本稿の目的は、実務に活用できるような形で制御理論について解説することです。制御理論を学ぶ際には、実際の回路をベースにするのではなく、ブロック線図を使用するケースがほとんどです。しかし、若干の数学と回路シミュレータの助けを借りれば、電子回路をベースとして制御理論について理解することが可能になります。
はじめに
大学では、「これを学んで就職の役に立つのか？」とも感じられる数多くの科目を教えています。制御理論についても、何ページにもわたる数式やフィードバック・システムのブロック線図を使って説明されることがほとんどでしょう。そのため、制御理論もすぐに役立つとは思えない科目の1つになっているかもしれません。しかし、実際には、制御理論は次のような問いに対する答えを技術者に示してくれます。
- 期待どおりに機能するシステムを設計するにはどうすればよいのか？
- システムが安定性を損なう可能性を見極めるためには何をすればよいのか？
- システムから最良の応答を得るにはどうすればよいのか？
機械、電気、土木、航空、通信など、大学には多くの分野を対象とした科目が用意されています。様々なことを学んだ結果、それぞれの分野で利用できそうなシステムを構築できるようになるかもしれません。しかし、出来上がったシステムが安定性を欠くもので、特定の条件下でしか機能しないとしたら、現実の世界では何の役にも立たないでしょう。
設計技術者にとって、制御理論は人生そのものであるかもしれません。
制御理論について書かれた優れたテキストはいくつもあります。ただ、その多くは、ブロック線図を使って説明を進める旧来のアプローチを採用しています。それに対し、本稿では電子工学を専門とする技術者向けに、回路の解析とシミュレーションの観点から電子制御の理論について説明していきます。具体的には、一般的な2次システムの背景にある理論を取り上げ、実際に動作する回路例をベースとして解説を加えることにします。2次システムの基礎についてわかりやすく解説することで、電子制御の理論を学ぼうとする人がアナログ回路設計との関連を理解してもらえるよう配慮します。なお、解説の中で示すシミュレーション結果は、アナログ・デバイセズの回路シミュレータ「LTspice®」を使用して取得しました。
2次システムの基本
最も基本的な2次システム（2次回路）の例を図1に示しました。
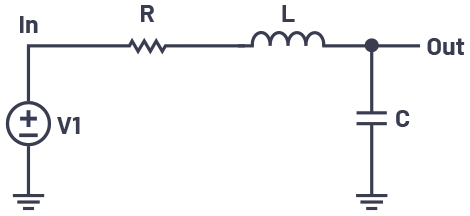
この回路の伝達関数は、次のようになります。
この式の右辺をご覧ください。分母の部分は特性多項式として知られています。この特性多項式をゼロとおくと、特性方程式が得られます。あるシステムにおいて、その伝達関数の分母がゼロに等しい場合には極が生じます。つまり、特性方程式の根（sの値）を求めれば、システムの極が明らかになります。その結果、そのシステムの動作について豊富な情報を得ることができます。
一般に、2次システムの伝達関数は次のような形になります。
ここで、ζは減衰係数、ωnはrad/秒を単位とする回路の固有振動数（非減衰振動数）です。
式（1）から、2次システムの一般的な特性方程式は次式のようになります。
式（1）と式（3）を比較すると、図1の回路の固有振動数は次式のようになることがわかります。
また、この回路の抵抗と減衰係数の間には、式（5）～（7）のような関係があることもわかります。
これらの式については直感的に理解することができるのではないでしょうか。つまり、回路に抵抗が存在しなければ損失（減衰）は生じないということです。その場合、回路に刺激（stimulus）を加えると、永久に振動し続けることになります。一方、値が大きい抵抗が存在すれば、振動は急激に減衰します。
図2に示したのは、1Vのステップ入力によってRLC回路を励起した場合の信号波形です（シミュレーション結果）。インダクタLの値を1µH、コンデンサCの値を1µFとし、抵抗Rの値を0Ω、100mΩ、500mΩに変化させています。この回路は、予想どおり159kHzの振動数で振動します。抵抗の値が大きくなると、減衰に対してどのような影響が及ぶのかはっきりと確認できます。
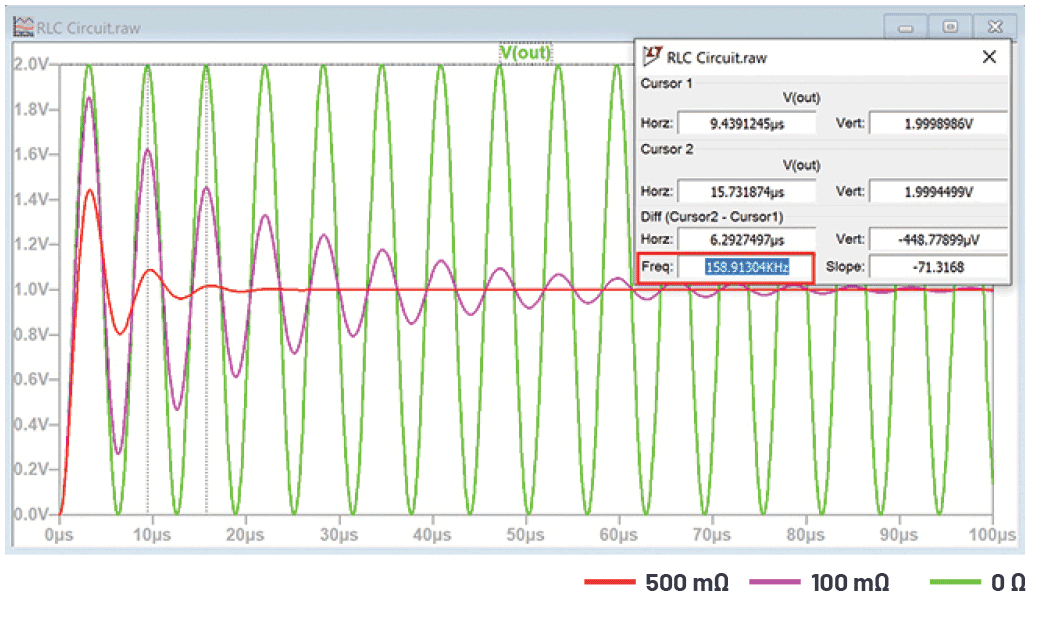
図2の振動については、ラプラス領域（s領域）から時間領域（t領域）への変換を実施することにより、数学的に表すことができます。ラプラス領域における単位ステップ入力は、次式で表すことができます。
したがって、2次システムを単位ステップ入力によって刺激した場合の応答は、次式のようになります。
部分分数展開を用いると、この式は次のように変形することができます。
この式はラプラス領域で表現されています。
これを時間領域で表すと、以下のようになります。
ここで、ωdの意味は以下のとおりです。
なお、逆ラプラス変換を用いて式（11）を導出する方法については、付録Aをご覧ください。
式（11）を見ると、図1の回路がステップ入力に対してどのように応答するのかを理解することができます。応答波形は正弦波のような性質を持っており、その振幅はe-ζωntの項で変調されます。つまり、振幅は減衰係数の正負に応じて、指数関数的に減衰／増大します。近似的に見れば、この応答は正弦波の部分と余弦波の部分から構成されるとも言えます。しかし、減衰係数が小さい場合には、正弦波の部分の影響が小さくなることがわかります。
この回路の固有振動数はωnです。しかし、この振動数で振動が起きるわけではありません。そうではなく、この回路は減衰係数ζによって決まるやや低めの振動数ωdで振動します。ωdは減衰固有振動数として知られています。一方、指数関数的な減衰は、回路の非減衰固有振動数ωnに依存します。
このシステムの極は、次式のように伝達関数の分母をゼロとおくことで求められます。
この式は、2次方程式の解の公式を用いることで解くことができます（以下参照）。
ここでa、b、cは以下のとおりです。
a = 1
b = 2ζωn
c = ωn2
システムの極は次の条件で生じます。
減衰係数が1未満である場合、平方根の中が負になってしまいます。したがって、式（15）は次式のように書く方が適切でしょう。
式（12）を使うと、式（16）は次のように書き換えることができます。
この式から、システムの極には実数部（-ζωn）と虚数部（±jωd）があることがわかります。
式（17）は、特性方程式の根（システムの極）を表しています。これらの極は、システムの安定性とどのような関連を持つのでしょうか。この点を明らかにするためには、ラプラス領域の極と時間領域の安定性を結びつける必要があります。
式（11）と式（17）から、以下のような知見が得られます。
まず、非減衰固有振動数ωnにより以下の事柄が決まります。
- ラプラス領域の極の実数部（- ζωn）……式（17）より
- 時間領域での指数関数的な減衰（e-ζωnt）……式（11）より
このことから、システムの指数関数的な減衰は極の実数部によって決まるという仮定が成り立つでしょう。
続いて、減衰固有振動数ωdによって以下の事柄が決まります。
- ラプラス領域の極の虚数部（± jωd）……式（17）より
- 振動の実際の振動数
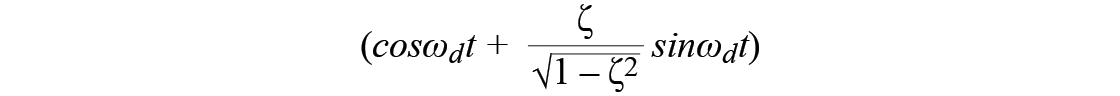……式（11）より
このことから、システムの実際の振動数は極の虚数部によって決まるという仮定が成り立ちます。
上記2つの仮定については、次に説明するs平面上で表現することができます。
安定なシステム
制御理論では、「s平面の左半分に極が存在する場合、そのシステムは安定である」とされます。図3は、x軸を実数部、y軸を虚数部としてプロットしたs平面の例です。
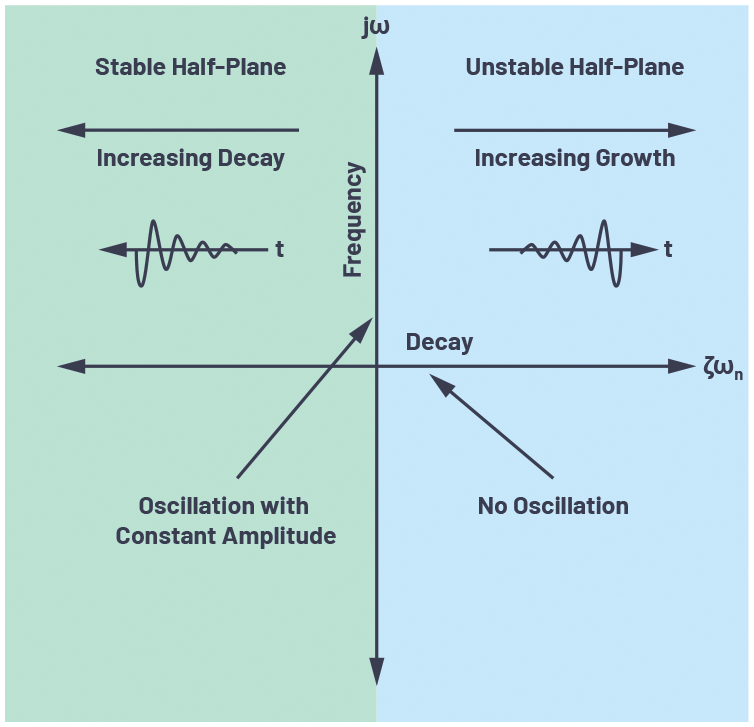
式（17）から、減衰係数が正（同式の実数部が負）である場合、極は左半面に存在することがわかります。減衰係数が増加するにつれて、式（17）の極は更に左の方（s平面の左半面の更に奥）へと移動します。
式（17）がラプラス領域にあるとすると、どのようにして時間領域に変換されるのでしょうか。
ここで式（11）を再掲します。
減衰係数ζが正の値である場合、振幅は指数関数的に減衰する応答（e-ζωntの項で決まる）を示します。減衰係数が大きいほど減衰は早くなります。減衰係数が増大すると、極はs平面の左半面（ラプラス領域）の更に奥へ移動し、時間領域における指数関数的な減衰量はより大きくなります。このことは、図2で確認することができます。図2に示したように、100mΩ、500mΩという抵抗値の違いによって、減衰量に影響が及びます。抵抗値が最も大きい500mΩの場合、減衰係数も最大になるので、指数関数的な減衰も顕著になります。一方、抵抗値が0Ωである場合、減衰係数はゼロになります。そうすると極はy軸上に存在することになり、図2で緑色の曲線で示したとおり、回路は永久に振動を続けます。
注目すべきは、システムが安定であっても、必ずしも振動が生じないとは限らないということです。この回路は、左半面に存在する極によって振動する可能性があります。ただ、図2に示したように、その振動の振幅は時間の経過に伴って減衰します。
図1の回路において、そのことは何を意味するのでしょうか。
この回路の減衰係数は、次式で与えられることがわかっています。
また、その固有振動数は次式のとおりです。
これらの式を使うと、Lが1µH、Cが1µFの場合、固有振動数は1Mrad/秒（159.1kHz）、Rが500mΩの場合の減衰係数は0.25になります。
したがって、減衰振動数ωdは次式で与えられます。
これを計算すると、減衰振動数は968krad/秒（154kHz）となります。これは、図4に示した赤色の波形の振動数に相当します。
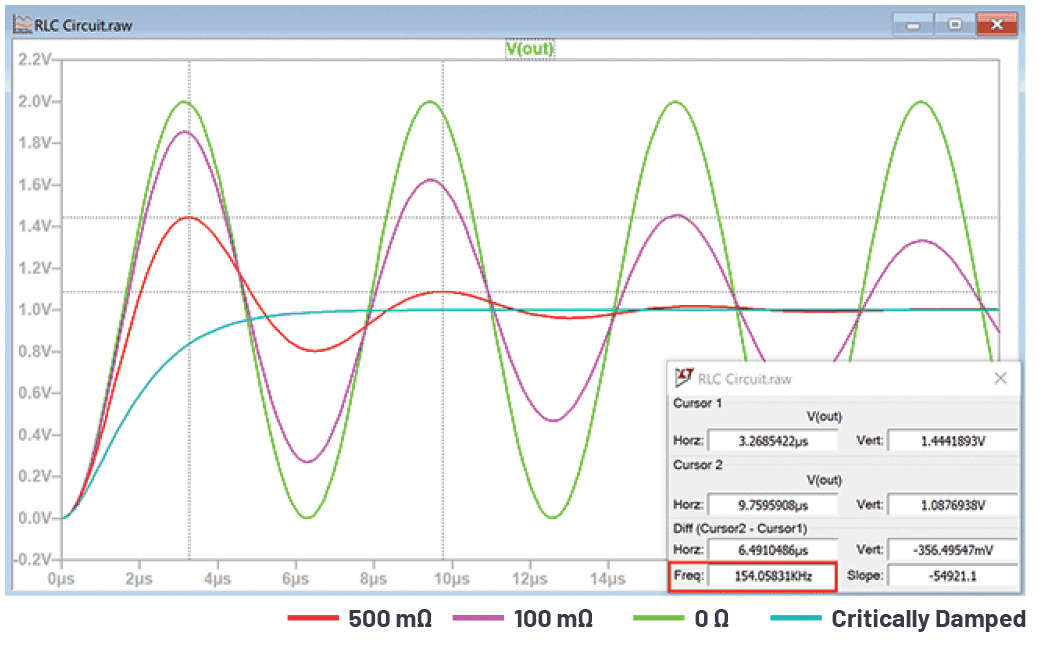
正弦波の振幅は、e-ζωntに従って減衰します。減衰係数が0.25、固有振動数ωnが1Mrad/秒、減衰固有振動数が968246rad/秒の場合、式（11）は次のようになります。
この式から、VOUTは3.26マイクロ秒の場合に1.44V、9.75マイクロ秒の場合に1.09Vと計算することができます。この結果は、図4に表示された値と一致しています。
図4には、減衰係数が増加することによる影響が明確に現れています。すなわち、振幅と減衰固有振動数の両方が減少しています。
では、減衰係数を増加させ続けると何が起きるでしょうか。
先述したように、減衰固有振動数は次式で表されます。
減衰係数を1まで増加させると、減衰固有振動数はゼロまで減少することがわかります。これは臨界減衰点として知られています。この条件で回路の振動が止まることは式（11）からもわかります。減衰固有振動数ωdがゼロまで減少すると、正弦項はゼロに、余弦項は1に等しくなります。そのため、式（11）は1次システムに相当する状態に簡素化されます（以下参照）。
つまり、抵抗を介してコンデンサを充電する場合と同様です。図4でも、臨界減衰の軌跡を確認できます。
不安定なシステム
どのような回路にも、抵抗は必ず存在します。多くの電子制御回路は、極が左半面に存在する状態になっており、本質的に安定です。ただ、式（11）から、減衰係数が負の値である場合には、振幅が指数関数的に増大することがわかります。つまり、右半面に極が存在していると不安定な状態になります。回路シミュレーションを行うと、負の抵抗を挿入することによって、右半面に存在する極の影響を簡単に確認することができます。シミュレーション用に用意した図5のRLC回路では、抵抗に負の値を設定しています。
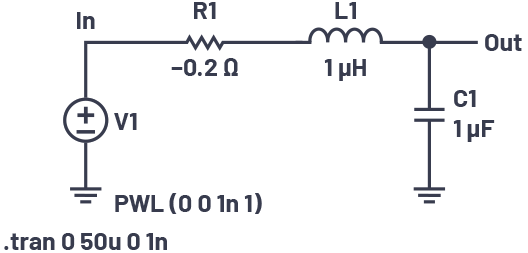
この回路の減衰係数は-0.1です。図6に、ステップ入力に対するこの回路の応答を示しました。
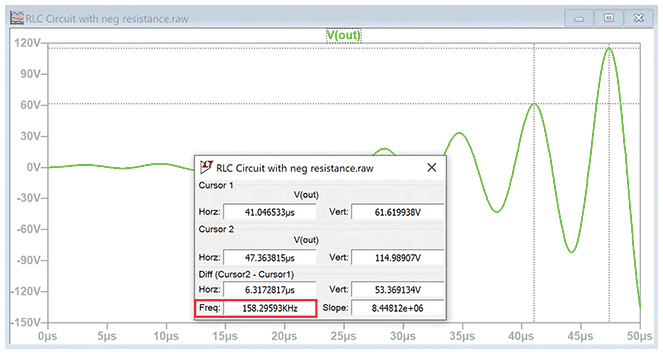
この場合も、減衰固有振動数は次式によって決まります。
減衰係数が-0.1の場合、実際の振動数は994987rad/秒（158.3kHz）です。
式（11）から、回路の応答は次式のようになります。
このように、出力が増大する場合の振幅応答も計算できます。VOUTは41.05マイクロ秒において61.62V、47.36マイクロ秒において114.99Vです。これらは、図6に表示されている値と一致しています。
主要極
システムに多くの極が存在する場合、解析が複雑になる可能性があります。しかし、極の間が十分に離れていれば、ある極の影響が他の極による影響と比べて支配的になるというケースが少なくありません。そうした場合、支配的ではない極を無視することで状況を単純化することができます。支配的な影響を及ぼす極のことを主要極（dominant pole）と呼びます。
ここで図7をご覧ください。この回路の上側には、LとCの値が等しい2つのRLC回路が配置されています。抵抗の値が小さい方の回路では、s平面の虚数軸の近くに極が生じます。
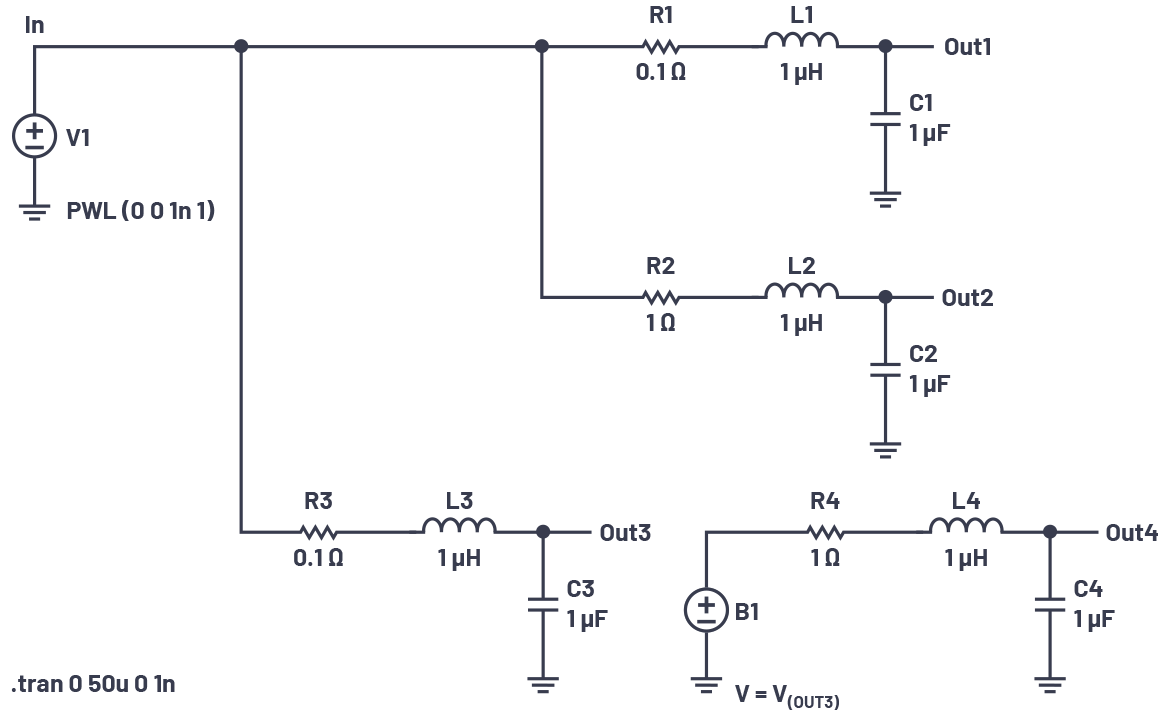
図7の下側の回路では、これら2つの回路を直列に配置しています。但し、V(OUT3)はビヘイビア電圧源B1を使用してOut3を複製することで得ています。これにより、R4、L4、C4がOut3の負荷になることを回避しています。そのため、V(OUT3)×V(OUT4)の真の応答を観測することができます。
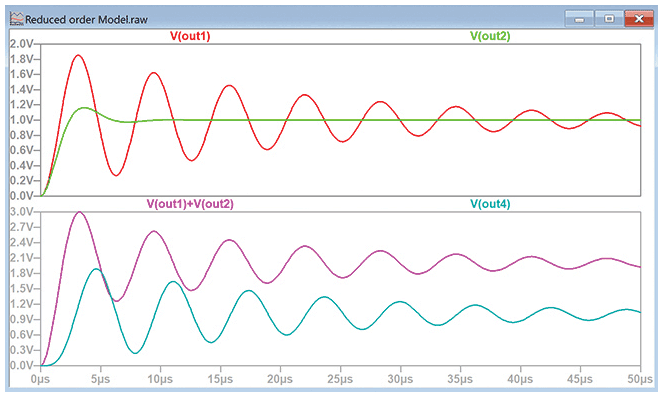
並列回路、直列回路それぞれの応答を図8に示しました。当然のことながら、抵抗値が最大の回路において減衰係数が最大になります。V(out2)のプロットを見ると、振動が最も早く減衰していることがわかります。ただ、2つの出力を加算（回路を並列に接続）または乗算（回路を直列に接続）した場合、V(out1)の応答が支配的になることがわかります。つまり、複雑なシステムを単純化するには、虚数軸に近い極を持っている回路に焦点を絞るとよいということです。その極の方が、システムの応答に対して支配的に働きやすいからです。
極が両半面に存在するシステム
ここまで、極が左右どちらかの半面に存在するシステムについて検討してきました。では、システムの極が左半面と右半面の両方に存在する場合にはどうなるのでしょう。安定性に関して言えばどちらの影響が大きいのでしょうか。なぜそうなるのでしょうか。
ここでもう一度、式（11）をご覧ください。そうすると、システムが安定であるか否かを決めるのは指数部であることがわかります。式（11）の正弦／余弦部は無視して指数部を見るだけで、左半面の極と右半面の極が組み合わさることにより何が起きるのかを把握することができます。図9は、そのことを実証するための単純な回路です。
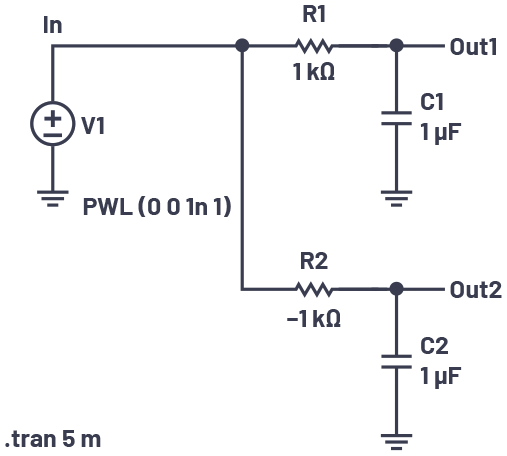
上側のRC回路では、正の値を持つ抵抗を使用しています。この場合、極が左半面にあることは明らかです。一方、負の値を持つ抵抗を使用した下側の回路では、極が右半面に生じます。これに関する数学的な導出方法については、付録Bをご覧ください。
図10に、図9の回路の応答を示しました。
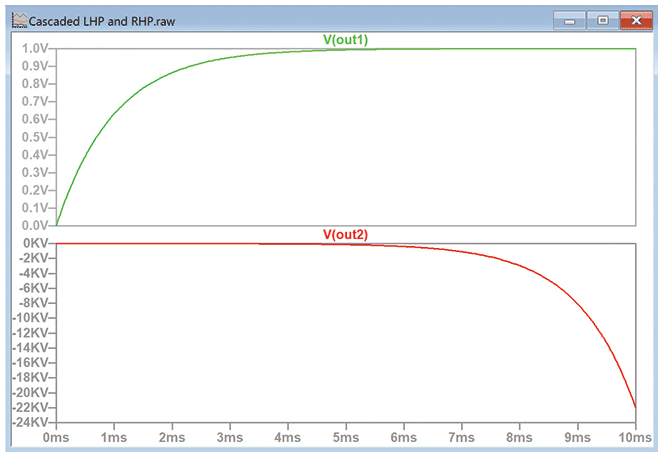
上側の波形を見ると、約5ミリ秒が経過した後は傾きがゼロに落ち着いています。一般に、RC回路の出力は時定数の約5倍で落ち着くと言われますが、そのとおりの動作を示しているということです。一方、V(out2）の曲線を見ると、傾きが増加し続けています。このことから、極が左半面にある回路と右半面にある回路を直列に接続した場合、明らかに回路全体としては不安定になることがわかります。なぜなら、極が左半面にある回路が安定したかなり後になって、極が右半面にある回路の応答が指数関数的に増加し続けることになるからです。つまり、回路が安定であるためには、すべての極が左半面に存在していなければなりません。
まとめ
本稿では、電子制御理論で用いられる理論的なモデルを、技術者が向き合っている現実の世界に結びつけることを目指しました。制御システムは、システム内の抵抗（減衰の要因）により、すべての極が左半面に生じる場合に安定になります。極が右半面に存在するシステムの応答を確認するには、負の抵抗をモデル化しなければなりません。そのことが原因で、解析において問題が生じる可能性があります。しかし、コンピュータ・シミュレーションの助けを借りれば、単に抵抗の値を正から負に変えるだけで安定な回路と不安定な回路の検証を実施できます。
ラプラス変換は、教室以外の場所では滅多に使うことはありません。ただ、本稿で示したとおり、2次システムがどのように動作するのかを理解する上では非常に役に立ちます。
付録A
ここでは、以下の2つの式が等価であることを示します。
単位ステップ入力のラプラス変換は、以下のように表されます。
2次のローパス・フィルタの一般的な伝達関数は、次式のようになります。
したがって、2次システムを単位ステップで刺激した場合の応答は、次式で表されます。
数学では、標準的な部分分数展開として以下のような式が使われます。
ここでxをsに置き換えます（以下参照）。
式（A4）を見ると、分子にはsやs2の項が存在しません。また、分母にはaの項がありません。
よって、式（A6）は次のように書き換えることができます。
更に、以下のように書き換えることが可能です。
ここで、両辺の分母を同じ形にするために次のように変形します。
確認のために、式（A9）の右辺と式（A8）の右辺を比較してみましょう（以下参照）。
ここで、式（A9）の両辺の分子が等しいとおくと、A、B、Cを求めることができます。
ここで、s2の係数同士が等しいとおくと、以下の式が得られます。
0 = A + B
次に、s1の係数同士が等しいとおくと、以下の式が得られます。
0 = A(2 ζω n) + C
更に、s0の係数同士が等しいとおくと、以下の式を得ることが可能です。
ωn2 = Aωn2
以上の式から、A = 1、B = -1、C = -2ζωnという結果が得られます。
したがって、式（A8）から次式が得られます。
（BとCは負なので、符号が変わっていることに注意してください）。
時間領域（左辺）からラプラス領域（右辺）への変換には、次の3つの式を適用できます。
ここで平方完成を適用することにより、式（A12）は次のように書くことができます。
これは次式のように変形できます。
ここで、分母の第1項に一致させるために分子が（s + ζωn）に等しくなるように変形し、次式に示すラプラスの恒等式を使えるようにします。
ζωnを単独の分数に分けることにより、式（A14）は次式のように変形できます。
a = -ζωn、b = ωn√(1 - ζ2)です。
次に、分母に一致させるために式（A17）の第3項の分子をωn√(1 - ζ2)に等しくなるように変形し、次式に示すラプラスの恒等式を使えるようにします。
式（A17）の第3項をωn√(1 - ζ2）で割ると、ωn√(1 - ζ2)を分子に置くことができます。
その結果、式全体を次のように書き換えることが可能になります。
a = -ζωn、b = ωn√(1 - ζ2)です。
これで、式（A19）をラプラス領域の式から時間領域の式に変換することができます（以下参照）。
上式の第3項については、ωnを約分することができます。また、減衰固有振動数ωdは次式で表されます。
したがって、式（A20）は次式のように単純化することが可能です。
多くの教科書では、式（A22）の多項式を次式のように書くこともできると説明しています。
ここで、β = √1 - ζ2、θ = tan-1(β/ζ)です。
以上で、減衰係数と非減衰固有振動数に依存する減衰指数関数と、減衰固有振動数に依存する振動の式が得られました。
式（A23）をスプレッドシートに入力すれば、ステップ入力に対する出力のグラフをプロットすることができます。
付録B
ここでは、以下の2つの式が等価であることを示します。
単位ステップ入力のラプラス変換は、次のように表されます。
一方、RC回路の伝達関数は、一般に次式で与えられます。
sが負の値である場合、分母はゼロに等しくなります。そのため、この回路の極は左半面に存在し、システムは安定です。抵抗の値が負である場合には、極が右半面に存在してシステムが不安定になります。
式（B3）から、ステップ入力に対するRC回路の伝達関数は、次式で与えられることがわかります。
数学では、以下のような部分分数展開が標準的に用いられます。
この場合、a = 0です。
したがって、以下の式が成り立ちます。
分子のs1の項同士が等しいとおくと、以下の式が得られます。
0 = ACR + B
分子のs0の項同士が等しいとおくと、以下の式を得ることができます。
1 = A
したがって、A = 1、B = -CRです。
そのため、以下の式が得られます。
時間領域（左辺）からラプラス領域（右辺）への変換には、次の2つの式を適用できます。
それにより、式（B7）を時間領域の式に変換すると、RC回路の応答は次式のようになることがわかります。
以上のように、期待どおりの結果が得られました。
補遺
本稿に関連するLTspiceのファイルをこちら からダウンロードすることができます。
なお、LTspiceの詳細についてはanalog.com/jp/ltspiceをご覧ください。
参考資料
1 Charles Phillips、Royce Harbor「Feedback Control Systems, 4th edition（フィードバック制御システム 第4版）」Prentice Hall International、1988年
謝辞
本稿で示した理論の校正を支援してくださったブルネル大学（ロンドン）のMaysam Abbod博士に感謝します。
