Read other articles in this series.
要約
ブリッジ回路は、抵抗やその他のアナログ値を正確に測定するための非常に有効な方法です。このアプリケーションノートは、パート1の続きであり、高信号出力のシリコン歪みゲージを実装したブリッジ回路を、アナログ-ディジタルコンバータ(ADC)に接続する方法を取り上げています。シグマデルタADCがこの方法の特徴であり、シリコン歪みゲージを利用するときに圧力センサを実装するための低コストな方法です。
はじめに
この話題のパート1であるアプリケーションノート3426 「抵抗ブリッジの基礎:パート1」では、抵抗ブリッジを使用する理由、ブリッジの基本構成について説明し、またボンディングワイヤや箔の歪みゲージで生成される小出力信号のブリッジについて説明しました。このアプリケーションノートでは、高出力のシリコン歪みゲージを対象にしています。すなわち、このパート2のアプリケーションノートでは、高出力のシリコン歪みゲージに焦点を当て、この歪みゲージと、高分解能のシグマデルタアナログ-ディジタルコンバータ(ADC)との適合性が極めて優れていることを説明しています。また、必要なADC分解能や非補償型センサのダイナミックレンジの計算方法についての実例を挙げています。このアプリケーションノートでは、ADCとシリコン歪みゲージの特性を活用することによって、より単純なレシオメトリック回路を作成する方法、および電流駆動センサを使用するアプリケーションのための簡単な回路を作成する方法を示しています。
シリコン歪みゲージのバックグラウンド
シリコン歪みゲージの利点は、その高い感度にあります。シリコン内の歪みによって、そのバルク抵抗が変化します。このため信号は、箔やボンディングワイヤの信号より1桁大きくなり、抵抗の変化は、抵抗器の寸法の変化によってのみ決まります。シリコン歪みゲージから大信号が得られるため、低コストの電子回路をゲージとともに使用することができます。ただし、この小さな壊れやすいデバイスに物理的にワイヤを実装して接続することはコストがかかって困難であるため、ボンディング歪みゲージのアプリケーションでの使用は限られています。それでもなお、シリコン歪みゲージは、MEMS (マイクロエレクトロメカニカルシステム)アプリケーションで最適なゲージです。MEMSを使用すると、機械構造物をシリコンで作ることが可能で、またこれらの機械構造物の一部として複数の歪みゲージを製造することができます。このように、MEMSプロセスを利用すると、全体的な設計問題に対する頑丈で低コストのソリューションが得られ、歪みゲージを個別に取り扱う必要がありません。
MEMSデバイスの最も一般的な例はシリコン圧力センサで、最初に普及したのは1970年代です。この圧力センサは、標準の半導体プロセスの手法と、これに加えて特殊なエッチング工程を利用して製造しています。特殊なエッチングによって、ウェハの裏面から選択的にシリコンを除去することで、強力なシリコンフレームで囲まれた何百もの正方形の薄膜ダイヤフラムが作成されます。ウェハの表面には、各ダイヤフラムの各エッジに、歪みに敏感な抵抗器が1つ埋め込まれます。金属トレースによって各ダイヤフラムのまわりの4つの抵抗器が接続され、フルアクティブのホイートストンブリッジが作成されます。次にダイヤモンドソーを使用して、個々のセンサをウェハから解放します。この時点で、センサは完全に機能しますが、使用する前に圧力ポートを取り付けてワイヤを接続する必要があります。この小さなセンサは、安価ですが比較的頑丈です。ただし、マイナス面もあります。センサは温度によって大きな影響を受けるため、初回のオフセットと感度に関して広い許容範囲が必要となります。
圧力センサの実例
具体的に説明するため、ここでは圧力センサを使用します。基本となる原理は、同じタイプのブリッジをセンサとして使用するいずれのシステムにも当てはまります。生の圧力センサの出力用の1つのモデルを式1に示します。式1の変数の大きさと範囲によって、与えられた圧力(P)に対して、広範囲にわたるVOUT値がもたらされます。同じ温度でもいろいろなセンサの間でVOUTの値はばらつきます。また、1つのセンサの中でも温度の変化に応じて値はばらつきます。始終一貫して意味のある出力を得るためには、各センサを較正し、製品間のばらつきや温度ドリフトを補償する必要があります。長年、キャリブレーションはアナログ回路で行われてきました。ただし、最新のエレクトロニクスによって、ディジタルのキャリブレーションもコスト的にアナログに対抗することができるようになり、ディジタルキャリブレーションによって得られる精度ははるかに優れています。2~3のアナログの「裏技」を使用することで、精度を犠牲にすることなくディジタルキャリブレーションを簡素化することができます。
VOUT = VB × (P × S0 × (1 + S1 × (T - T0)) + U0 + U1 × (T - T0))
ここで、VOUTはブリッジの出力、VBはブリッジ励起電圧、Pは加えられる圧力、T0は基準温度、S0はT0における感度、S1は感度の温度係数(TCS)、U0は圧力を加えない状態でのT0におけるブリッジのオフセットまたは不均衡、およびU1はオフセット温度係数(OTC)です。
式1は、1次多項式を用いてセンサをモデル化しています。多くのアプリケーションに対応するには、より高次の多項式、区分線形手法、あるいは係数用の参照テーブルを用いた区分2次近似を使用することが必要になると思われます。使用するモデルにかかわらず、ディジタルキャリブレーションでは、VOUT、VB、およびTをディジタル化する機能が必要であり、またすべての係数を決定して必要な計算を実行する方法も必要となります。式2は、Pを解くために式1を並び替えたものです。式2は、ディジタル計算(一般的にはマイクロコントローラ(µC)が行う)によって正確な圧力値を出力するために必要な情報をより明確に示しています。
P = (VOUT/VB - U0 - U1 × (T-T0))/(S0 × (1 + S1 × (T-T0))
総当り回路
図1の回路に示す総当り方法は、1つの高分解能ADCを使用して、VOUT (AIN1/AIN2)、温度(AIN3/AIN4)、およびVB (AIN5/AIN6)をディジタル化しています。次にこの測定値がµCに送信され、そこで実際の圧力が計算されます。ブリッジは、ADC、電圧リファレンス、およびµCと同じ電源からじかに電力が供給されます。抵抗温度検出器(RTD) (回路図ではRtで表されています)は、温度を測定します。ADCの入力MUXは、ブリッジ、RTD、または供給電圧の測定に対応しています。キャリブレーション係数を求めるために、システム全体(または少なくともRTDとブリッジ)をオーブンに配置し、較正済みの圧力源によってブリッジに圧力を加えながら、いくつかの温度で測定を行います。次に、テストシステムによって測定データを処理し、キャリブレーション係数を求めます。得られた係数はµCにダウンロードされて、不揮発性メモリに格納されます。
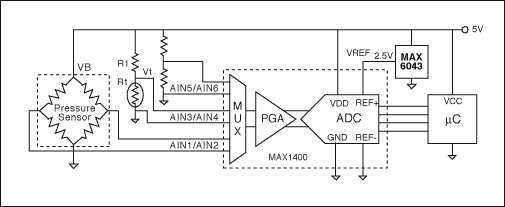
図1. 回路は、実際の圧力を計算するのに必要な変数(励起電圧、温度、およびブリッジ出力)をじかに測定します。
このような回路を設計する際の重要な検討事項は、ダイナミックレンジとADC分解能です。最小要件は、アプリケーション、および使用するセンサとRTDの正確な仕様に左右されます。具体的に説明するため、以下の仕様を使用します。
システムの仕様
- フルスケール圧力:100psi
- 圧力分解能:0.05psi
- 温度範囲:-40°C~+85°C
- 電源:4.75V~5.25V
圧力センサの仕様
- S0 (感度):150~300µV/V/psi
- S1 (感度の温度係数):-2500ppm/°C (最大)
- U0 (オフセット):-3~+3mV/V
- U1 (オフセット温度係数):-15~+15µV/V°C
- RB (入力抵抗):4.5k
- TCR (抵抗の温度係数):1200ppm°C
- RTD:PT100
- Alpha:3850ppm/°C (ΔR/°C = 0.385Ω公称)
- -40°Cでの値:84.27Ω
- 0°Cでの値:100Ω
- 85°Cでの値:132.80Ω
- PT100の詳細については、マキシムのアプリケーションノート3450 「正帰還によってPT100トランスデューサを補償」を参照してください。
電圧の分解能
最小許容電圧分解能は、検出可能な最小圧力変化に対する、VOUTの最小応答によって決まります。この状態が生じるのは、最小供給電圧で最大温度における最小感度センサを使用するときです。式1のオフセット項は、分解能を決定する要因ではないことに留意してください。分解能は圧力に対する応答によってのみ決まるからです。
式1と上記のしかるべき仮定を使用すると、次のようになります:
ΔVOUT min = 4.75V (0.05psi/カウント 150µV/V/psi × (1+ (-2500ppm/°C) × (85°C -25°C)) ≈ 30.3µV/カウント
したがって:ADC最小分解能 = 30µV/カウント
入力範囲
入力範囲は、最大可能入力電圧と、最小入力電圧(または最大負電圧)によって決定されます。式1でVOUTの最大値を生み出す条件は以下のとおりです。 最大圧力(100psi)、最小温度(-40°C)、最大供給電圧(5.25V)、3mV/Vのオフセット、-15µV/V°CのオフセットTC、-2500ppm/°CのTCS、最大感度のチップ(300µV/V/psi)。最大負信号は、圧力が加えられていない状態(P = 0)、5.25Vの供給電圧、-3mV/Vのオフセット、-40°Cの温度、+15µV/V°CのOTCの状態で生じます。
再び、式1と上記のしかるべき仮定を使用すると、次のようになります。
VOUT max = 5.25V × (100psi · 300µV/V/psi × (1+ (-2500ppm/°C) ×
VOUT min = 5.25 × (-3mV/V + (0.015mV/V/°C × (-40°C - 25°C))) - -21mV
したがって、ADC入力範囲 = -21mV~+204mVになります。
ビット分解能
このアプリケーションで使用するADCの公称値は、入力範囲が-21mV~+204mVで、電圧分解能が30µV/カウントです。このADCのカウントの総数は、(204mV + 21mV)/(30µV/カウント) = 7500カウント、すなわち、13ビットのダイナミックレンジよりわずかに少ないものとなります。センサの出力範囲がADCの入力範囲と正確に一致するのであれば、13ビットのコンバータによってこのアプリケーションの要件を満足できることになります。-21mV~+204mVは、一般的なADCの入力範囲には一致しないため、入力信号をレベルシフトして増幅するか、あるいは高分解能のADCを利用する必要があります。幸いにも、高分解能でバイポーラ入力の、アンプを内蔵した最新のシグマデルタコンバータによって、高分解能のADCを実用的に使用することができます。これらのシグマデルタADCは経済的なソリューションであり、部品を追加する必要はありません。これによって、基板サイズが小さくなるだけでなく、これまで必要であった増幅とレベルシフトのための回路に伴うドリフト誤差も解消されます。
5V電源で動作する標準的なシグマデルタコンバータは、2.5Vのリファレンスを使用し±2.5Vの入力範囲を備えています。今回の圧力センサアプリケーションにおける分解能の要件を満たすためには、ダイナミックレンジが、2.5V - (-2.5V)/(30µV/カウント) = 166,667カウントのADCが必要となります。これは17.35ビットの分解能が必要であるということであり、18ビットの MAX1400などの、多くのADCの能力の範囲内です。SARのADCを必要とする場合、11ビットの結果を生み出すために、18ビットコンバータを13ビットアプリケーションで使用することは極めてぜいたくなことになります。しかし、たとえ3つのMSBを基本的に使用しないとしても、18ビット(17ビットと符号)のシグマデルタコンバータを使用することは非常に実用的です。手頃な価格に加えて、シグマデルタコンバータは、高入力インピーダンスと優れたノイズ除去の機能も備えています。
18ビットADCに代わる別の手法として、増幅器を内蔵する低分解能のコンバータ(16ビットのMAX1416など)を使用するという方法があります。8の内部利得を選択すると、ADCの読み取り値をMSBに向かって3ビットだけシフトすることが可能となり、これによってすべてのコンバータのビットを使用して、コンバータの要件を15ビットに低減することができます。利得のない高分解能コンバータと利得のある低分解能コンバータのいずれかを選択するときには、適用できる利得と変換レートにおけるノイズを必ず考慮してください。シグマデルタコンバータの有効な分解能は、そのノイズによって制限されることが多くなります。
温度の測定
温度を測定する理由が圧力センサの補償のためだけであるならば、温度の測定は正確である必要はありません。必要なことは、各測定値に対応した固有の温度が再現されるということです。これによって、高度な柔軟性と余裕のある設計基準が可能となります。基本的な設計要件は3つあります。すなわち、「自己発熱を防止すること」、「適切な温度分解能があること」、および「ADCの測定範囲を超えないこと」です。
最大圧力信号に近いVtに対して最大電圧を選択すると、温度と圧力の測定で同じADCと内部利得を使用することができるようになります。この例では、最大入力電圧は+204mVです。抵抗器の許容誤差に対応できるよう、最大温度電圧として控えめに+180mVを選択することも可能です。Rtの両端の電圧を+180mVに制限すると、Rtの自己発熱に伴う問題も解消されます。最大電圧の選択が完了すれば、VB = 5.25Vのとき85°Cにて最大電圧を示すR1の値を計算します(Rt = 132.8Ω)。R1は式3を用いて計算することができます。ここでVtmaxはRt両端の最大許容電圧です。温度分解能は、ADCの電圧分解能を温度とともに変化するVtで除算することによって得られます。式4は、温度分解能の計算を示しています(注:この例では、計算した最小電圧分解能を使用しているため、控えめな設計となっています。実際のノイズのないADC分解能を使用することも可能です)。
R1 = Rt × (VB/Vtmax - 1)
R1 = 132.8Ω × (5.25V/0.18V - 1) ≈ 3.7kΩ
TRES = VRES × (R1 + Rt)²/(VB × R1 × ΔRt/°C)
ここで、TRESは温度測定の分解能であり、単位は「°C/ADCのカウント」になります。
TRES = 30µV/count × (3700Ω + 132.8Ω)²/(4.75V Ω 3700Ω × 0.38Ω/°C) ≈ 0.07°C/カウント
ほとんどのアプリケーションでは、0.07°Cの温度分解能で十分です。ただし、より高分解能が必要な場合には、いくつかのオプションが利用可能です。たとえば、「より高分解能のADCを使用する」、「RTDをサーミスタに置き換える」、あるいは「ブリッジ回路でRTDを利用し、ADC内部でより高利得を使用することができるようにする」などがあります。
有用な温度読み取り値を得るためには、供給電圧のいかなる変化もソフトウェアが補償することが必要です。別の手法として、R1をVBでなくてVREFに接続するという方法があります。これによって、VtはVBに依存しなくなりますが、同時に電圧リファレンスに対する負荷が増大することになります。
少し緩やかな総当り
シリコン歪みゲージとADCには、図1に示した回路を簡素化することのできるいくつかの特性があります。式1から、ブリッジの出力は供給電圧(VB)に正比例していることがわかります。この特性を備えたセンサはレシオメトリックセンサと呼ばれています。式5は、誤差が温度に依存する、すべてのレシオメトリックセンサのための一般式です。式5は、式1におけるVBより右側のすべての項を汎用関数ƒ(p,t)で置き換えたものであり、pは測定対象の特性の強度、tは温度です。
VOUT = VB × ƒ(p,t)
ADCにもレシオメトリック特性があります。すなわち、出力は、入力電圧とリファレンス電圧の比率に正比例しています。式6は、入力信号(Vs)、リファレンス電圧(VREF)、フルスケール読み取り値(FS)、およびスケールファクタ(K)で表した、汎用ADCのディジタル読み取り値を示しています。スケールファクタは、アーキテクチャの種類やあらゆる内部増幅に対処するためのものです。
D = (Vs/VREF)FS × K
ADCの性能は、式6のVsに、式5の右辺(VOUTに相当する項)を代入することによって求めることができます。結果は、次の式7になります。
D = (VB/VREF) × ƒ(p,t) × FS × K
式7では、VB対VREFの比率が重要であって、その絶対値は重要ではありません。したがって、図1に示した回路の電圧リファレンスは不要となります。ADC用の電圧リファレンスは、VB/VREFの一定比率を維持する単純な抵抗分圧器によって得ることができます。この変更によって、電圧リファレンスが不要となるだけでなく、VBを測定する必要もなくなり、またVBの変動を補償するために必要なすべてのソフトウェアも不要となります。この手法は、すべてのレシオメトリックセンサで機能します。Rtと直列にR1を配置することによって作成された温度センサもレシオメトリックであるため、温度測定についても電圧リファレンスは不要となります。この回路を図2に示します。
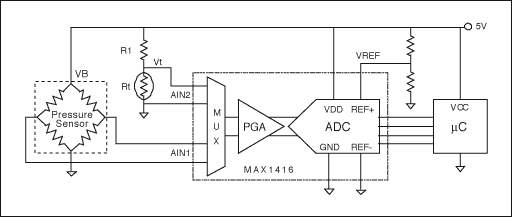
図2. レシオメトリック回路の例。圧力センサの出力、RTD電圧、およびADCのリファレンス電圧は、すべて供給電圧に正比例しています。これによって、絶対電圧リファレンスが不要となり、実際の圧力を求めるために必要な計算が簡素化されます。
RTDの排除
シリコンベースの抵抗器は、温度に対して非常に敏感です。この特性を利用して、システムの温度センサとしてブリッジ抵抗を使用することができます。これはコストを低減するだけでなく、より優れた結果も得られます。RTDと、ストレスに敏感なブリッジとの間に存在していたと思われるいずれの温度勾配も排除できるからです。前述したように、温度測定の値に再現性があって固有な値である限り、温度測定の絶対精度は重要ではありません。固有であるという要件があるため、温度検知の方法は、圧力を加えたときにインピーダンスが一定のまま維持されるブリッジに限定されます。幸いにも、大部分のシリコンセンサは、この要件を満たすフルアクティブブリッジを使用しています。
図3は、ブリッジの低電圧側と直列に抵抗器(R1)を配置することによって、温度に依存する電圧を生成する回路です。この抵抗器を加えることによって、ブリッジ両端の電圧と、したがってその出力も低減します。これは通常、大きな電圧低下ではありませんが、利得を増大させたりリファレンス電圧を減少させたりするのには十分です。式8を使用すると、R1の控えめな値を計算することができます。これは、R1 < RB/2のときによく機能し、ほとんどのアプリケーションに当てはまります。
R1 = (RB × VRES)/(VDD × TCR × TRES - 2.5 × VRES)
ここで、RBはセンサブリッジの入力抵抗、VRESはADCの電圧分解能、VDDは供給電圧、TCRはセンサブリッジの抵抗の温度係数、およびTRESは所望の温度分解能です。
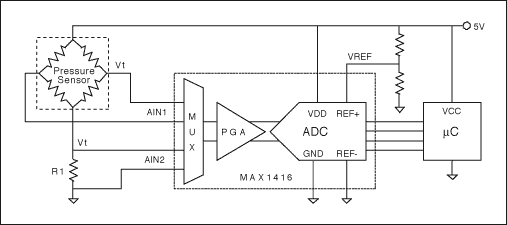
図3. 圧力測定のためにブリッジ出力を使用し、温度測定のためにブリッジの抵抗を使用するレシオメトリック回路の例。
上の例を続行し、0.05°Cの温度分解能、R1 = (4.5kΩ × 30µV/カウント)/(((5V × 1200ppm/°C × 0.05°C/カウント) - 2.5) × 30µV/カウント) = 0.6kΩを仮定します。R1はRBの1/2未満であるため、この結果は有効です。この例では、R1を追加することで、VBが12%低下されます。ただし、コンバータを選択する際に、分解能を17.35ビットから18ビットに切り上げることが必要となりました。これによって、VBの低減を補償する以上に分解能が増大します。
温度が増加するにつれて、ブリッジの抵抗は上昇し、両端の電圧は低下します。温度に伴うVBのこの変化によって、TCS項が生成されます。幸いなことにこの項はプラスであり、センサ固有のTCSはマイナスであるため、センサと直列に抵抗器を配置することによって、補償されていないTCSの誤差が実際に減少します。上記のキャリブレーション手法は引き続き有効です。必要なことは、若干の小さな誤差を補償するだけです。
電流駆動のブリッジ
定電流センサまたは電流駆動センサと呼ばれる、特殊クラスのシリコン圧電抵抗センサが存在します。これらのセンサは、電流源で駆動されるとき、温度に対して感度が一定(TCS ≈ 0)となるように特別に処理されています。オフセット誤差やOTC誤差をなくす、あるいは大幅に低減させるために特別な抵抗器を加えることは、電流駆動センサでは一般的なことです。センサを較正するには、基本的にアナログ手法が使用されています。これを使用することで、設計者は、温度や圧力に対してあらゆる部分を測定するという費用のかかる作業から解放されます。広い温度範囲にわたる、これらのセンサの絶対精度は一般に、ディジタル的に較正されたセンサほど良好ではありません。これらのセンサの性能を向上するために引き続きディジタル手法を使用することが可能で、ブリッジ両端の電圧を測定することで容易に温度情報を得ることができます。これは一般的に、2000ppm/°Cを超える速さで増大します。図4の回路は、ブリッジに電力を供給する電流源を示しています。定電流を確保するために使われるのと同じ電圧リファレンスがADCのリファレンス電圧にも供給されています。

図4. この回路は、従来方式の電流源によって電力が供給される電流駆動センサを使用しています。
電流源の排除
電流駆動センサによってSTCを補償する方法がわかれば、図5の回路によって、電流源を含めることなく、図4の回路と同じ結果を得ることができるようになります。ただし、電流駆動センサには引き続き励起電圧(VB)が存在するため、VBは電圧供給によって確定されません。VBは、ブリッジの抵抗とブリッジを流れる電流によって決まります。前述したように、シリコン抵抗器は正の温度係数を持ちます。このため、ブリッジが電流源から電力を供給されると、VBは温度の上昇とともに増大することになります。ブリッジのTCRが、TCSと大きさが同じで符号が反対の場合、VBは、低減する感度を補償するために適切な速さで温度とともに増大し、TCSは限定された温度範囲に対してほぼゼロになります。
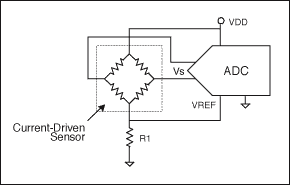
図5. 回路は、電流駆動センサを使用していますが、電流源または電圧リファレンスを必要としません。
図4の回路におけるADCの出力のための式は、式7のVBをIB x RBに置き換えることによって得ることができます。これは式9になります。ここで、RBはブリッジの入力抵抗で、IBはブリッジを流れる電流です。
D = (IB × RB/VREF) × ƒ(p,t) × FS × K
図5に示した回路は、電流源または電圧リファレンスを使用することなく、図4の回路と同じ性能を発揮することができます。これは、2つの回路の出力を比較することによってわかります。図5のADCの出力は、式7のVBとVREFに適切な式を代入することによって求まります。これは式10になります。
式7の繰返し:D = (VB/VREF) × ƒ(p,t) × FS × K
図5の回路では、VB = VDD x RB/(R1 + RB)、 およびVREF = VDD x R1/(R1 + RB)となります。
式7にこれらを代入すると、式10が得られます。
D = (RB/R1) × ƒ(p,t) × FS × K
VREF/IBに等しいR1を選択した場合、式9と10は同一になります。したがって、図5の回路は、図4の回路と同じ結果になることがわかります。同一の結果であるためには、R1がVREF/IBに等しくなければなりません。ただし、これは適正な温度補償を得るための必要条件ではありません。RBに温度に依存しない定数を掛け合わせる限り、温度補償が得られることになります。R1の値は、システムの要件に最適に合致するように選択することができます。
図5の回路を使用するときに忘れてはならないことは、ADCのリファレンス電圧は温度とともに変化するということです。このため、他のシステムの電圧を監視するにはADCは適していません。実際には、追加の補償のために温度に敏感な測定が必要になる場合は、特別なADCチャネルで供給電圧を測定することによってこの測定を得ることができます。また、図5の回路を使用するときには、VREFがADC用に指定した範囲を超えないように注意することも必要です。
結論
シリコン圧電抵抗の歪みゲージは、比較的大きな出力であるため、低コストで高分解能のシグマデルタADCにじかに接続することができます。これによって、増幅とレベルシフトの回路に伴うコストと誤差を解消することができます。また、これらの歪みゲージの熱特性とADCのレシオメトリック特性を利用することで、高精度の回路の複雑さを大幅に低減することができます。
{{modalTitle}}
{{modalDescription}}
{{dropdownTitle}}
- {{defaultSelectedText}} {{#each projectNames}}
- {{name}} {{/each}} {{#if newProjectText}}
-
{{newProjectText}}
{{/if}}
{{newProjectTitle}}
{{projectNameErrorText}}




















