ピーク電流モードと連続電流モードのDC/DCコンバータのモデリングおよびループ補償設計に関する考慮事項
コンピューティングなどの多くのアプリケーションでは、パワー・レールの負荷過渡応答条件が次第に厳しさを増しています。更に、複雑なラプラス伝達関数の計算が含まれているため、ループ補償設計は多くのエンジニアにとって、複雑で時間を要する作業とみなされることがしばしばあります。
コンピューティングなどの多くのアプリケーションでは、パワ本稿では、広く用いられているピーク電流モード(PCM)と連続電流モード(CCM)のDC/DCコンバータの平均小信号モデリングについて、順を追って説明します。数学モデルと共に、スイッチング回路のシミュレーション・ツールであるアナログ・デバイセズのADIsimPE/SIMPLISを使用して、複雑な計算作業を最小限に抑えます。その結果、単純化されたモデルを示し、簡素で高速なループ補償設計とシミュレーションを実行します。最後に、ADP2386EVAL評価ボードのテスト結果を使用して、ループ・クロスオーバー周波数、位相マージン、負荷の過渡応答についてのシミュレーション結果がテスト結果と十分一致することを示します。ー・レールの負荷過渡応答条件が次第に厳しさを増しています。更に、複雑なラプラス伝達関数の計算が含まれているため、ループ補償設計は多くのエンジニアにとって、複雑で時間を要する作業とみなされることがしばしばあります。
PCM平均小信号モデリング
図1に示すように、6個のブロック(帰還抵抗分圧器、補償ネットワーク、電流検出およびサンプリング、コンパレータ、電力段、出力ネットワーク)が電流モードDC/DCコンバータの機能遂行に関わります。ループにおいて、インダクタの電流ランプ信号が、出力電圧からフィードバックされる補償エラー・アンプ出力と比較されます。PWM信号が生成され、インダクタ電流を変調するスイッチが駆動されます。インダクタ電流は、出力コンデンサと負荷に流入します。この6個のブロックのうち、電力段だけが非直線性のブロックで、DC/DCのモデリングにとって最も難しいブロックになります。

図 1. 電流モード降圧のブロック図
電力段を次の3端子スイッチとしてモデル化します。
- アクティブ・スイッチ・モード(A)
- コモン・モード(C)
- パッシブ・スイッチ・モード(P)、図2に示すように、次の式1が得られます。


図 2. 3端子スイッチの平均小信号モデル
これは連続電流モードでのみ有効な平均モデルで、巻き数比が1:dのトランスと等価です。このモデルによって、次の微分方程式2が得られます。
![]()
小信号 ![]() は平均モデルで使用され、平均小信号モデル(ASSM)となっています。このモデルによって電力段を直線化して、解析に用いることができます。
は平均モデルで使用され、平均小信号モデル(ASSM)となっています。このモデルによって電力段を直線化して、解析に用いることができます。
引き続き、PCM CCM降圧を例に用いると、図3に示すように、レギュレータ全体はラプラス伝達関数ブロック図でモデル化されています。電圧ループと電流ループの2通りの制御ループがあります。電流ループではインダクタ電流がRTで検出され、サンプリングされてコンパレータの最初の負入力のランプ波形になります。電圧ループでは、出力電圧のリップルが、ゲインKの抵抗分圧器で検出され、サンプリングされて補償ネットワークAv(s)に向けられ、コンパレータの正入力に入力されるエラー電圧となります。スロープ補償ランプ波形を第2の負入力信号として、コンパレータはデューティ・サイクルが調整された信号を生成して電力段の平均小信号モデルに入力し、インダクタ電流を変調します。

図 3. PCM CCM DC/DC制御モデルのブロック図
インダクタ電流から出力電圧へのゲイン関数は、式3で表せます。

PWMデューティ・サイクルからインダクタ電流へのゲイン関数は、式4で表せます。

コンパレータのゲインFmは、式5で表せます。ここで、Snはインダクタ電流の増加の傾き、Seはスロープ補償、Tsはスイッチング周期です。

サンプリング効果のゲイン関数は、式6で表せます。

入力電圧からインダクタ電流へのゲイン関数は、式7で表せます。

電流ループ・ゲイン関数は、式8で表せます。

電圧ループ・ゲイン関数は、式9で表せます。
![]()
ループ・ゲイン関数は、式10で表せます。

DC/DCループ・ゲインを設計する目的上、考慮すべき事項が4つあります。
- 低DC誤差のための高DCループ・ゲイン
- 高速過渡応答のための広いループ帯域幅
- 高い位相マージン(>45°)のためのクロスオーバー周波数付近での−20dBのスロープ
- ノイズ減衰のための高周波数での高い減衰量
レギュレータ・ループでは、補償器Av(s)と帰還抵抗分圧器Kのみを、設計者はカスタマイズできます。そのため、ループの設計には2つの手順があります。まず、式11で表されるオープンループ・ゲインを得るため、抵抗分圧器を出力から切り離します。

次に、オープンループ・ゲインGoc(s)のゼロとポールを補償する補償器Av(s)を設計し、目標のループ・ゲインが得られるようにします。
図4に、Ti>>1、 ![]() の場合の通常の負荷条件での例を示します。低周波数領域では、1つのポール(½πRoCo)と1つのゼロ(½πRcCo)があり、サンプリング効果He(s)を要因として、1つの2次のポール(1/πfs)が高周波領域にあります。補償器Av(s)は、クロスオーバー周波数を拡大し、クロスオーバー・ポイント付近での−20dBスロープを確保し、45°を上回る位相マージンが得られるよう設計されます。補償器には2つのポールと1つのゼロがあります。1つのポールはオープンループ・ゲイン・コンデンサのESRをゼロに補償するために使用され、他のポールはループのDCゲインを増大するための積分器として機能します。ゼロ・ポールはオープンループの負荷効果を補償します。高周波数での2次のポール(1/πfs)はノイズの減衰に有効です。
の場合の通常の負荷条件での例を示します。低周波数領域では、1つのポール(½πRoCo)と1つのゼロ(½πRcCo)があり、サンプリング効果He(s)を要因として、1つの2次のポール(1/πfs)が高周波領域にあります。補償器Av(s)は、クロスオーバー周波数を拡大し、クロスオーバー・ポイント付近での−20dBスロープを確保し、45°を上回る位相マージンが得られるよう設計されます。補償器には2つのポールと1つのゼロがあります。1つのポールはオープンループ・ゲイン・コンデンサのESRをゼロに補償するために使用され、他のポールはループのDCゲインを増大するための積分器として機能します。ゼロ・ポールはオープンループの負荷効果を補償します。高周波数での2次のポール(1/πfs)はノイズの減衰に有効です。

図 4. PCM CCM DC/DCループの設計手順
SIMetrix/SIMPLISで補強されたADsimPEツールは、アナログ・デバイセズのリニア製品やスイッチング製品を評価するのに最適な個人版の回路シミュレータです。SIMetrixはオペアンプなどのリニア回路に非常に有用で、SIMPLISはDC/DCコンバータやPLLなどのスイッチング製品をターゲットとしています。図5では、回路動作とモデルの精度をチェックするためのリファレンスとして、PCM CCM降圧リファレンス回路が設定されています。これは、入力が3.3V、出力が1.2V、スイッチング周波数が1.2MHzのPCM同期降圧レギュレータです。

図5. PCM CCM降圧SIMPLISのリファレンス回路
図6の左側に、平均小信号モデルでのループ・ゲインの計算結果を示します。クロスオーバー周波数は50kHz、位相マージンは90.35ºです。図6の右側に示すSIMPLISシミュレーションの結果では、クロスオーバー周波数が47.6kHzのときに90.8°の位相マージンとなることが示されています。これにより、ADIsimPE/SIMPLISスイッチング回路シミュレーションの結果が複雑なASSM計算の結果と一致し、設計者にループ設計のための高速な手段が提供されることが示されました。ただし、回路図は図5に示すように、それほど単純とは言えません。ple.

図6. ASSMの計算結果とSIMPLISのシミュレーション結果
PCMの簡略化された平均小信号モデリング
アプリケーションではクロスオーバー周波数が1√LCoよりはるかに大きいことを考慮すると、複雑な式でも概略値を計算することができます。式4で、PWMデューティからインダクタ電流へのゲイン関数は、式12のように簡略化できます。

図3から、式13に示すように、補償器の出力電圧からインダクタ電流へのオープンループ・ゲイン関数を導くことができます。

Seは、補償スロープの立上がりエッジのスロープです。
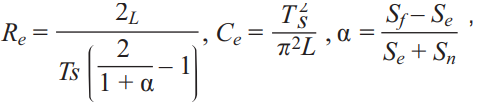
上式とし、更に、クロスオーバー周波数が1√LCoよりはるかに大きいので、式13のオープンループ・ゲイン関数は更に簡略化でき、式14のようになります。

その結果、オープンループASSMは図7に示すように簡略化され、補償された出力電圧で制御される電流源からインダクタ電流を生成するRLCネットワークに電流が流入するというモデルになります。これは元の複雑な式に比べ、シミュレーションや計算がはるかに容易なモデルです。

図 7. 簡略化されたASSMオープンループ回路
図5のリファレンス回路を使用し、ReとCeを計算して、図8に示すように、クローズドループの簡略化されたASSM回路をADSimPEに設定します。SIMetrixのシミュレーション結果を図8の右側に示します。クロスオーバー周波数が49kHz、位相マージンが90.5°で、これはセクション2で示したASSMの計算結果およびSIMPLISのシミュレーション結果とよく一致しています。

図8. 簡略化したASSMシミュレーション回路と結果
ADP2386のモデリング・シミュレーションとテスト結果
ADP2386は、アナログ・デバイセズの同期型PCM CCM降圧レギュレータです。20Vの入力電圧を、最大6Aの出力電流で0.6Vの出力電圧に降圧します。スイッチング周波数範囲は、200kHz~1.2MHzです。このデバイスの汎用性により、コストやサイズを増加させることなく、降圧アプリケーションや反転昇降圧回路で使用することができます。このセクションでは、ADP2386EVAL評価用ボードを使用して、モデル・シミュレーションの結果を検証します。ループ・テストと負荷過渡応答テストの2通りのテストを比較します。
ADP2386EVALの回路図を図9に示します。テストでは、下の表1の行1に示す条件でボードが設定されています。ADP2386の内部スロープ補償は![]() のデューティ・サイクルに適応可能で、式14を用いて、表1の行2に示すように簡略化したASSMパラメータが得られます。出力コンデンサのDCバイアス仕様は3.3V時には約30%低下するため、簡略化したASSMシミュレーションでは、出力コンデンサの値を評価用ボードの147µFではなく、100µFに変更しています。
のデューティ・サイクルに適応可能で、式14を用いて、表1の行2に示すように簡略化したASSMパラメータが得られます。出力コンデンサのDCバイアス仕様は3.3V時には約30%低下するため、簡略化したASSMシミュレーションでは、出力コンデンサの値を評価用ボードの147µFではなく、100µFに変更しています。
| VIN | VO | FS | IO | L | C | 補償器 |
| 12 V | 3.3 V | 600 kHz | 3 A | 2.2 μH | 147 μF/5 Ω | 44.2 kΩ, 1.2 n, 4.7 p |
| RT | Se | Sn | Sf | Re | Ce | Gm |
| 123 mΩ | 0.2 V/μs | 0.49 V/μs | 0.18 V/μs | 2.51 Ω | 128 nF | 580 μS |

図9. ADP2386EVALの回路図
図10に、ADP2386EVALループの簡略化したASSMシミュレーションとテスト結果を示します。左側はADISimPD/simetrixによるシミュレーションで、クロスオーバー周波数は57kHz、位相マージンは71°です。右側はAPのModel 300でのテスト結果で、クロスオーバー周波数は68.7kHz、位相マージンは59.3°です。テスト結果とモデル・シミュレーションの間には相違がありますが、ADP2386のデータシートによると、そのエラー・アンプのゲインはインダクタと出力コンデンサの不正確さと組み合わさり、380μS~580µSの幅があることがわかります。したがって、この2つの結果の差異は許容可能なものです。

図10. ADP2386EVALループのシミュレーションとテスト結果
負荷過渡応答テストには2種類のテストがあります。テスト1は、表1に示した十分な位相マージンと広いクロスオーバー周波数の補償器条件で実施したものです。テスト2は、補償器を100pF/1.2nF/44.2kΩに変更したもので、クロスオーバー周波数を39kHz、位相マージンを336°に下げたものです。図11は、負荷過渡応答(0.5A~3A、0.2A/μs)テスト1のシミュレーションとテスト結果を示すものです。オーバーシュートのピーク値は、テストで67mV、シミュレーションで59mVとなり、応答曲線は良好に一致しています。図12は、負荷過渡応答(0.5A~3A、0.2A/µs)テスト2のシミュレーションとテスト結果を示すものです。オーバーシュートのピーク値は、テストで109mV、シミュレーションで86mVとなり、応答曲線は同様に非常によく一致しています。

図11. ADP2386EVAL負荷過渡応答テスト1のシミュレーションとテスト結果

図12. ADP2386EVAL負荷過渡応答テスト2のシミュレーションとテスト結果
まとめ
ループ補償は、高速の負荷過渡応答アプリケーションの場合はとりわけ大変な設計作業と見なされています。本稿では、広く用いられているピーク電流制御モードの連続電流降圧デバイスに基づき、平均小信号の数学的なモデリングおよびループ計算とADISimPE/SIMPISの高速で使いやすいシミュレーション手法の概要を示しました。更に、簡略化した平均小信号モデルを紹介し、ループ補償の設計処理を簡便に行う方法を示しました。ADP2386EVAL評価用ボードのループと負荷過渡応答のベンチ・テストによって、この簡略化したモデルとそのシミュレーションの精度が実証されました。