オンラインシミュレータによるバックコンバータ出力誤差バジェット分析の検証

要約

バックコンバータの予想される出力電圧精度は、負荷電流ステップに対する過渡応答の大きさの推定値によってある程度決まります。負荷状態でのバックコンバータの電圧降下の大きさを、簡単な手計算とマキシムのオンラインEE-Sim^® DC-DCコンバータ設計ツールを使って推定し、推定を実行するための各種の方法と、それぞれに関連する精度のレベルをテストします。

はじめに

あるバックコンバータの設計で、出力電圧誤差バジェット分析を実施する必要がありました。誤差の最大の要因は、負荷ステップによって生じる出力電圧降下です。電圧降下を推定するための各種の方法を試したところ、異なる結果になりました。どう考えたらよいのでしょう？このデザインソリューションでは、バックコンバータ出力誤差バジェット分析を行います。電圧降下の大きさの推定で、シミュレーション結果と2つの異なる概算による推定値を比較し、異なる方式のすり合わせを行います。

誤差バジェット

この計算では、バックコンバータの重要なパラメータは以下のとおりです。

V_IN = 5V、V_OUT = 3.3V

V_OUTのDC精度2%以内 = 66mV以内

バックコンバータを定義するその他の要素は以下のとおりです。

クロック周波数 = 695kHz

L = 2.7µH、C = 2 × 22µF

このバックコンバータの設計は、オンラインEE-Sim DC-DCコンバータ設計ツールで作成したものです。このツールによって提供されるシミュレーション結果は、以下のことを示しています。

V_OUTのリップル = 2.6mV_P-P または ≈ ±1.3mV (図1)

V_OUTの過渡電圧降下(1Aから2A時) = 157mV (図2)

したがって、最悪の場合の誤差バジェット(出力電圧の負の偏位)の推定値は次のようになります。

V_ERROR = 66 + 157 + 1.3 = 224.3mV

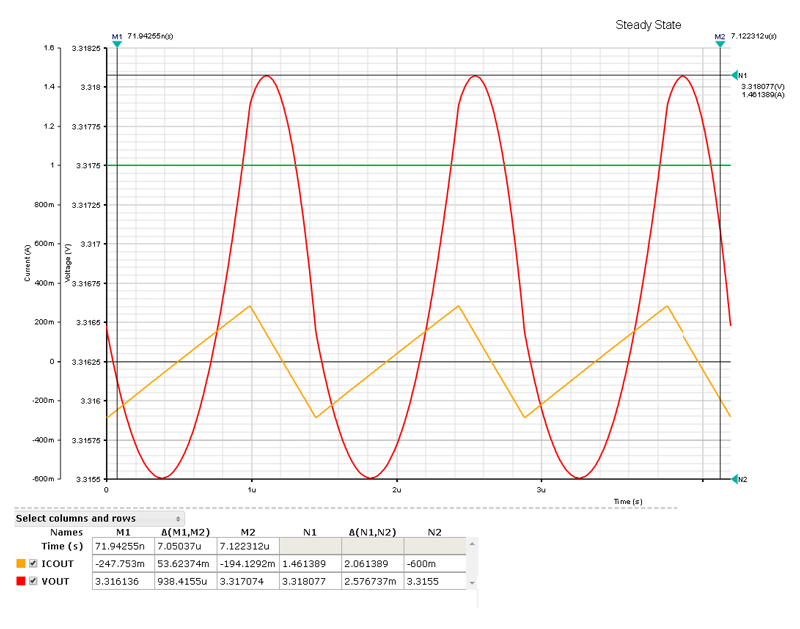図1. 出力電圧リップル(赤)とコンデンサ電流(黄)

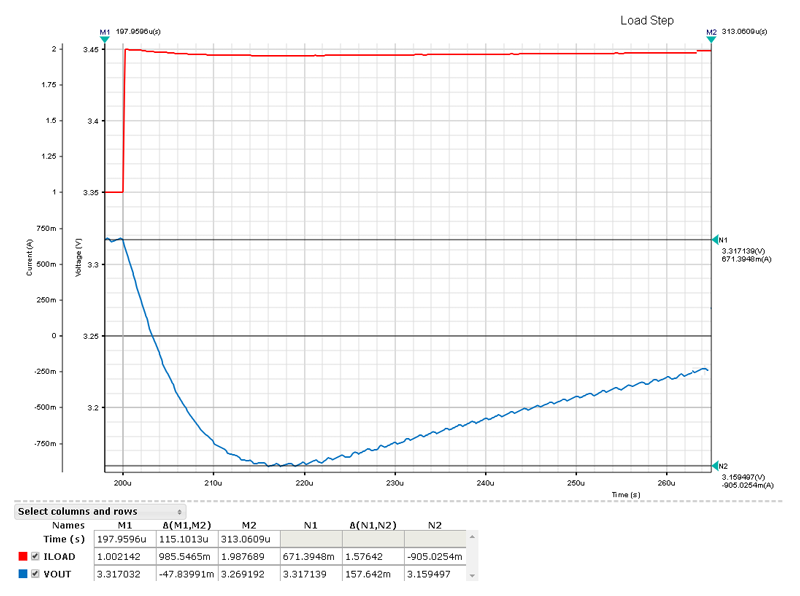図2. 負荷ステップ(赤)と応答(青)

224.3mVという誤差の推定値に対して、所定の誤差バジェットの目標は240mVです。これで問題はありませんが、なぜ結果が手計算と一致しないのでしょう？

CdV/dtの手計算による推定値

ここで、Iは負荷ステップ(1A)、Cは出力コンデンサ(2 × 22µF)、f_BWはレギュレータのクローズドループ帯域幅です。クローズドループ帯域幅f_BWは、クロック周波数の数分の1を設定値として使うことができます。図3では、オンラインシミュレーションを使用しました(18.8kHz)。

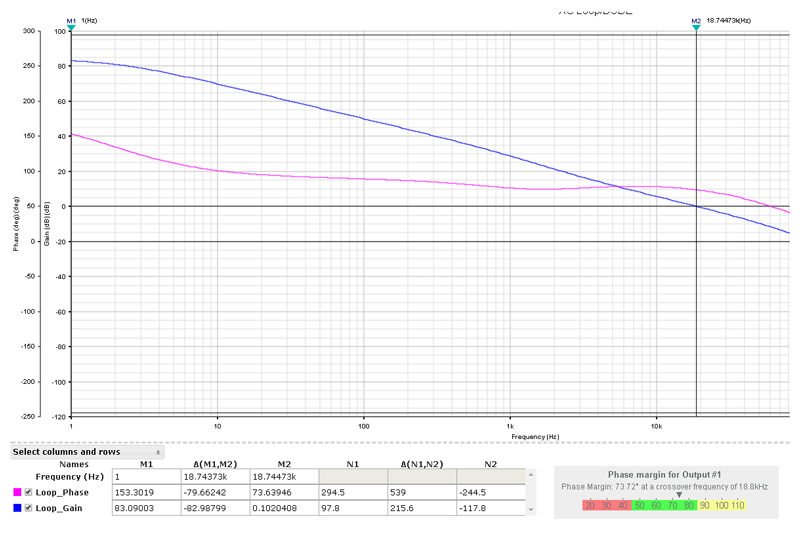図3. クローズドループ帯域幅(青)と位相マージン(紫)

この式の理論的根拠は、負荷ステップが急峻である場合にはコンデンサがすべてを負担し、次の法則に従ってリニアに放電するということです。

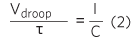
ここで、τは放電時間です。コンデンサの放電は、クローズドループ帯域幅f_BWの逆数に比例する遅延後にループが応答するまで続きます。

式(3)を式(2)に代入することによって、式(1)が得られます。この式によって、電圧降下の推定値は次のようになります。

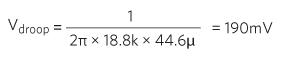
通常とは異なる容量値(44.6µF)が使われていることに注意してください。これは、高密度セラミックコンデンサの容量は印加する電圧によって大幅に変化するためです。ここでは、デバイスのメーカーによって提供されEE-Sim設計ツールによって使用されているデータに基づいてバイアスがV_OUT (3.3V)での実際の容量を使用しています。その結果、総誤差は次のようになります。

V_ERROR = 66 + 190 + 1.3 = 257.3mV

257.3mVは240mVのバジェットを上回っています。この推定値は問題です。最初は、式の理論的根拠は正しいように思えたのですが、何がいけないのでしょう？

LC共振の概算推定値

最初に気付くのは、この式がインダクタ(2.7µH)の存在を完全に無視していることです。ループの無応答時間の間、出力は本質的に図4に示すLC共振回路になります(SIMPLIS^®のシミュレーション)。

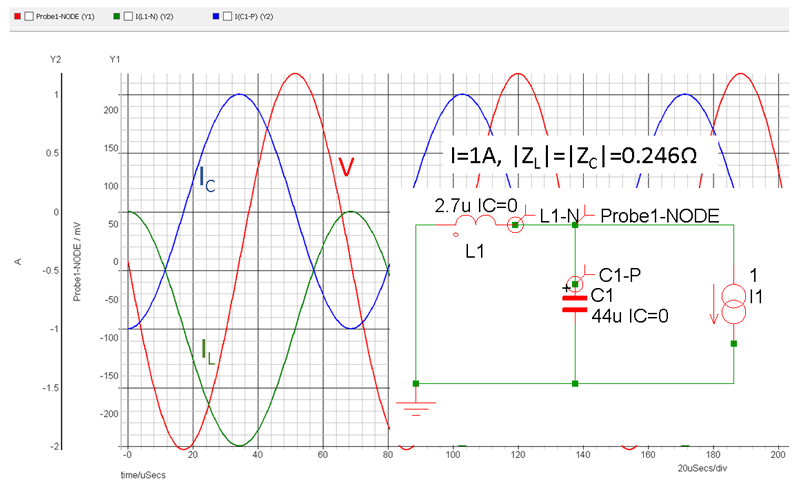図4. 電流ステップに対するLC共振応答

この場合、回路は振幅の発振を起こす傾向があります。

v = ZI sin⁡ 2π × f_RES × t

ここで、tは時間、Iは1Aの負荷ステップで、その他は以下のとおりです。

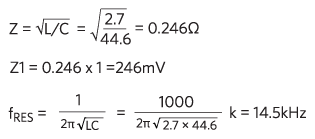
当然、この発振が起きるのは式(3)によって与えられる遅延時間τ後にループが応答するまでの間のみです。したがって、正弦波は次の電圧で止まります。

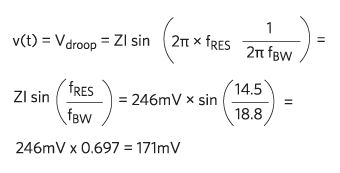
インダクタを含めて考えると、電圧降下の推定値は171mVになり、シミュレーション結果の157mVに大幅に近づきます。電圧降下の推定値が171mVの場合、誤差は238.3mVで、まだ240mVのバジェット内です。

すり合わせ

シミュレーションの実施または回路を作成して電流負荷ステップ発生器で動作させる以外に、2つの式を使って電圧降下の大きさの1次推定値を見つけることが可能で、1つは線形化電圧降下モデルの式です。

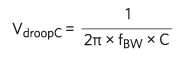
本格的なシミュレーションまたはブレッドボード作成の代わりに、どちらの式を使うべきでしょう？よくあることですが、それは場合によりけりです。f_RES << f_BWの場合は、sin x ≈ xという近似をV_droopLCの中で使用することによって、次式になります。

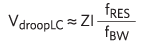
さらにZおよびf_RESにそれぞれの式を代入することによって、次式になります。

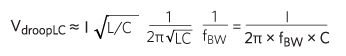
f_RES << f_BWの場合は、どちらの式でもうまく行きます。図5は、2つの方式の差および線形化誤差を示しています。

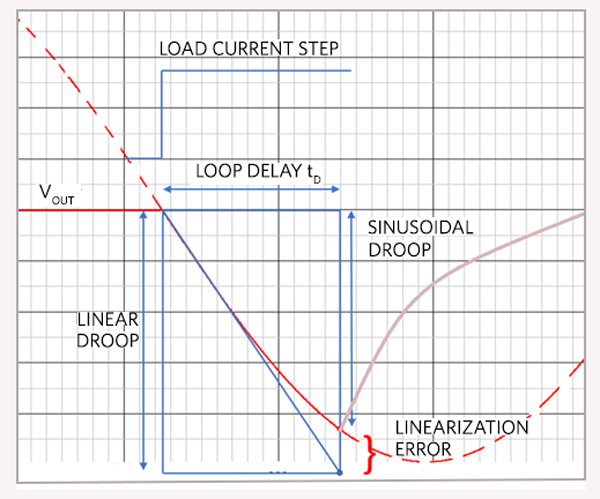図5. LC共振モデルと線形モデル

今の例の場合、2つの周波数が非常に近いため、CdV/dtベースの近似ではうまく行きません。

シミュレーションの優位性

EE-Sim設計ツールはSIMPLISを使用して回路の性能をシミュレートします。SIMPLISは、DC-DCコンバータなどのスイッチング回路のシミュレーション用に開発され最適化されています。上記の簡単な概算とは異なり、シミュレーションは回路のすべての要素(あるいは少なくとも部品のモデルに含まれているすべての要素)を計算に入れます。当然ながら、手計算は簡素化された式による大まかな推定値であり、回路のすべての効果は含まれず、部品の寄生成分(たとえばESRなど)は無視しています。そのため、シミュレーションは最も高精度の結果を提供します。

結論

MAX17242バックコンバータの設計用に出力電圧誤差バジェット分析を行いました。リップルおよび負荷ステップ電圧降下が誤差に及ぼす影響を、EE-SimオンラインDC-DCツールを使用してシミュレートしました。最初の手計算による電圧降下の概算は、シミュレーションに比べると悲観的なものでした。前提を見直し、ステップ応答計算に対するより高精度の概算方式に発展させました。この方式による結果は、シミュレーションの結果に大幅に近づきました。この結果とさらに重要度が高い点としてシミュレーションの結果によって、誤差バジェットへの適合に関する当初の懸念が軽減されました。

参照

EE-Sim^® DC-DCコンバータ設計ツール

セラミックコンデンサの温度および電圧変動

このデザインソリューションは、最初にHow2PowerTodayの2018年1月号に掲載されました。